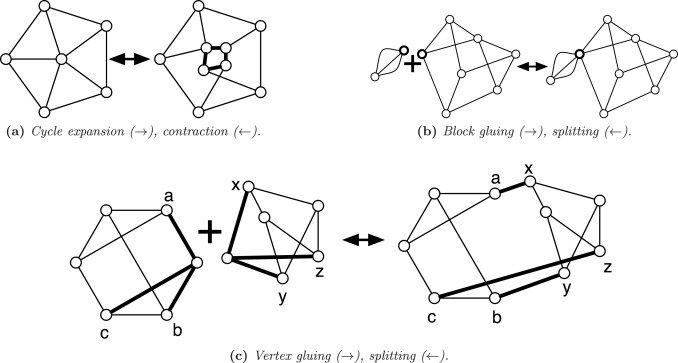
A multigraph is uniformly 3-edge-connected if there are exactly 3 edge-disjoint paths between any pair of vertices. For example, a uniformly 3-edge-connected graph is obtained from a 3-edge-connected graph by collapsing the nodes connected by more than edge-disjoint paths into supernodes. We characterize the class of uniformly 3-edge-connected graphs, giving a synthesis involving two operations by which every uniformly 3-edge-connected multigraph can be generated. Slightly modified syntheses give the planar uniformly 3-edge-connected graphs and the uniformly 3-edge-connected graphs with the fewest possible edges, generalizing the well-known Harary graphs. In proving the correctness of the synthesis, we also show the existence of a particular type of induced, non-separating cycle in near 3-regular graphs, which is of interest in its own right.